The two's complement
What time is it? Now it is time to talk about the two's complement.
This is not a topic that belongs to the original diary as well as not a
topic that I normally would discuss, because I prefer not to repeat concepts
that you can learn on the internet as I did. In early winter 2018, however,
I was talking with a friend of mine who was learning C/C++ from a book. He,
as me, has no software or electronic engineering background and he
was finding it difficult to understand datatype. How could a CHAR be
the same as an UNSIGNED INTEGER? How a SIGNED INTEGER is
different from an UNSIGNED one? The problem is that you must know a
little bit what goes on behind the scene (at a binary level so to say) to
learn C/C++ and the book he was reading didn't explain that, leaving my
friend frustrated and confused. In the end, I took a piece of paper and a
pencil and I explained to him what the two's complement is. So since I was
explaining that to him, why shouldn't I do the same with you: in a virtual
manner, you are also friends of mine, hence I create this extra post.
Before going just to the topic let me say, and forgive me for what I say,
that I don't like C and it is even worst with C++. If you ask me why, I
answer: "because they are not good!". About this, I am as my
5-year-old boy that says he doesn't like cheese, and if I ask him why, he
just answers me "because cheese is not good" without giving any extra
argument. When I was 5 years old I didn't like cheese too, and now as an
adult I like it; probably my experience has to grow to let me appreciate
C/C++, but for the moment I just don't like it. I know that, sooner or
later, the point will come when I have to study C/C++ seriously because I need
to read and understand software written by people that are so good in this
field that it is important to be able to read their work but I keep
deferring it.
To begin the explanation of the two's complement I have to say that
numbers are not infinite for a PC (laying on an endless line) but finite
laying in a circle like a watch. We have 12 hours on a watch and an AM/PM
flag to account for the 24 hours of the day. We count hours in the following
way. Starting at 2:00 AM we add 7 hours and we get 9:00 AM; we add 7 hours
more, we get 4:00 PM and toggle the AM/PM flag; we add 7 hours more and we
reach 11:00 PM; finally we add 7 hours more, we toggle the AM/PM flag again
and we end at 6:00 AM. We keep going round and round the circle every time
toggling the AM/PM flag when we cross 12. The CPU does the same. To keep the
explanation of the two's complement simple, I will consider a nibble
(that is half of a byte). A nibble is just a nibble: four binary digits. The
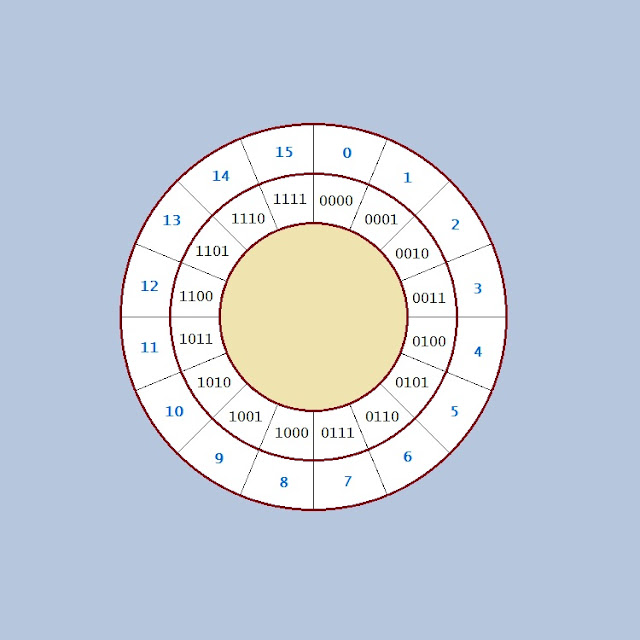
magic is how do we interpret these digits (Fig. A).
|
| Fig. A - Circle of numbers. |
The CPU counts in the circle of numbers, in the very same way as we do with the watch. Let's start at 7 and add 6 we get 13. If we add 6 once more, we set the "carry flag" to signal that we start the circle again, and we get 3. The association between the 16 states of the nibble with the numeric values from 0 to 15 is one of the possible association: the most natural one, because we interpret the digits in the binary base and we associate the equivalent decimal value for it, but it isn't the only association possible. The two's complement is another association that places all negative number where that most significant bit is set starting from 0 and counting counterclockwise (Fig. B).

|
| Fig. B - Two's complement circle of numbers. |
The innermost ring shows the binary representation of the nibble, the
outermost ring shows the hexadecimal representation of the nibble and the
other two rings represent the signed and unsigned integer representation. In
the two's complement representation, every time the most significant
bit is set (marked in red) the number is interpreted as negative. If you
want to see in a glance if any hexadecimal number is either positive or
negative interpreted in two's complement notation, you just have to
look at the most significant nibble and if it is between 0x8 and 0xF it is
negative. For instance, I know that 0xB045 is negative in a glance, even if
I don't know its exact value until I calculate it.
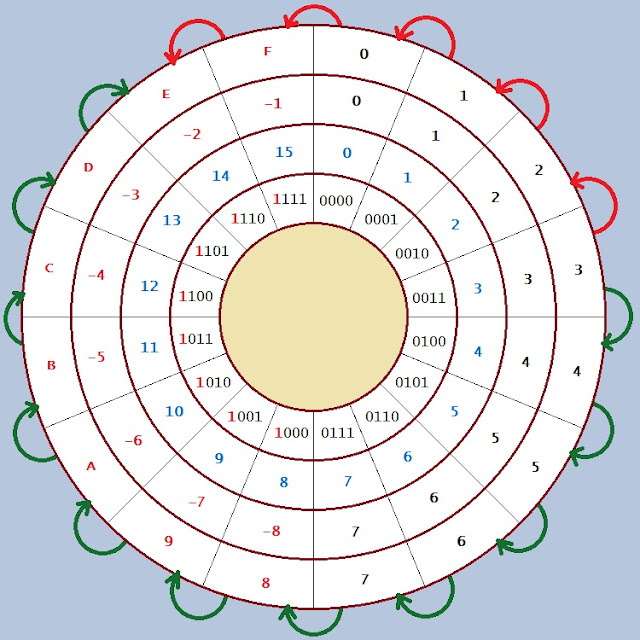
Addition and subtraction in two's complement works in the following
way: 3 - 5 = 3 + (-5). We see that -5 is equivalent to 11, so adding 11 to 3
gives back the same result as subtracting 5 from 3 (Fig. C).
|
| Fig. C - 3 minus 5. |
Subtraction is calculated with an addition. It is like Cristoforo Colombo that wanted to reach India from Spain but travelling the other way around the earth. In the book "But How Do It know" on page 140 we see the Arithmetic and Logic Unit that performs subtractions using the full adder circuit.
If you draw the circle as
Fig. B
you know immediately how to convert numbers back and forward because you read
immediately the values, but drawing the full circle for one byte is big and
for 16-bit crazy. So we use an algorithm instead of a draw, to convert back
and forward positive to negative numbers. The algorithm is the description of
the picture and tells us that we have a broken symmetry. A fully symmetric
draw would perfectly mirror left and right half having two times the
representation of +0 (= 0000 in binary) and -0 (= 1111 in binary)
and every number would face perfectly its opposite one, so that 7 faces -7, 6
faces -6 and so on1. The full symmetric draw wastes two states (0000 and 1111) for the same
information (+0 and -0). To avoid waste the left half of the circle is shifted
one step clockwise so that -1 get in the position of -0, -0 disappears and -8
comes in. Finally, the conversion algorithm says:
jump to the opposite way symmetrically (apply a logic NOT to the initial
binary number) and then make one more step clockwise to account for the
slight asymmetry. Let's try looking together at
Fig. B: 3 (0011) jumps symmetrically in the position of 12 (1100) but
here we find -4 instead of -3 because of the broken symmetry, so we move one
step clockwise (add one) and we find -3 (1101). Let's try the opposite
conversion from the draw: -5 (1011) jumps symmetrically in the position
of 4 (0100) but then we have to move again one step clockwise to account
for the broken symmetry (again we add one) and we finally find 5 (0101).
If you play the game with 0 and -8 you return to the start point so that 0
converts back to 0 and -8 converts back to -8. There is an opcode that
implements this algorithm: NEG. Now that you saw the draw and you know why -8
converts back to -8, you also understand why INTEL writes in the
8086 manual
(page 2-36) that negating -128 returns -128 and negating -32768 returns
-32768. It's a completely different feeling to read and accept what is in the
manual or really knowing the machinery behind it.
Before going to DEBUG and doing some experiments with what we have learned
until now, I have to extend the draw from nibble to byte and word. I cannot do
it for the complete circle, but I will do it just for the region around zero
in such a way that I can show you graphically what otherwise goes under the
name of sign extension.

|
| Fig. D - Section of the circle of numbers. |
Looking at Fig. D, I want you to observe that the less significant nibble follows the pattern as in Fig. B: and all other significant nibbles are just 0xF (or 1111 in binary). So when changing the size of the block of memory that we want to use to store our information you keep the most significant bit and just copy it or extend leftwards (the same is true in the clockwise direction so for positive numbers, you extend the 0). This is important because when I play with DEBUG I don't have 4 bits registers, so I must understand how to look at registers and check in a glance what is going on without the need of calculating it back in decimal.
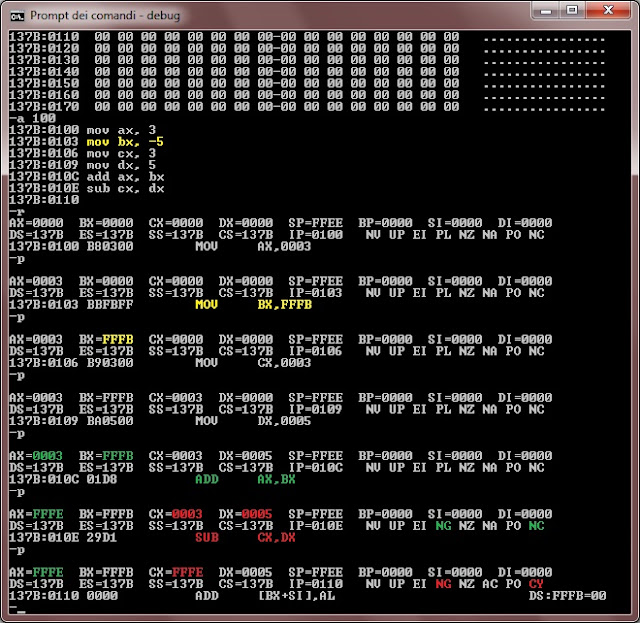
|
| Fig. E - 3 minus 5 in DEBUG. |
Fig. E shows my experiment with DEBUG to prove what I drew in Fig. C. I set AX = CX = 3, BX = -5 and DX = 5 then I did ADD AX, BX (AX = AX + BX -> AX = 3 + (-5)) and SUB CX, DX (CX = CX - DX -> CX = 3 - 5). Observe how DEBUG converts -5 into 0xFFFB (in yellow) and notice that -5 on 16-bit is just the same as -5 on 4-bit with the sign estention (0xB -> 0xFFFB). As you can see both results are the same (again 0xFFFE is 0xE of Fig. C with the addition of the sign estention). Please notice that when we go counterclockwise (red steps in Fig. C) we cross the top and in fact the SUB operation triggers the carry flag in Fig. E (marked also in red). This is the very last aspect that I want you to observe and be aware of: crossing the top of the circle sets the carry flag. If we change the example a little bit and performs 7 - 5 we see that we cross the top of the circle in the clockwise direction (when we perform 7 + (-5) marked with green in Fig. F) and in DEBUG the ADD sets the carry flag (marked also with green in Fig. G).
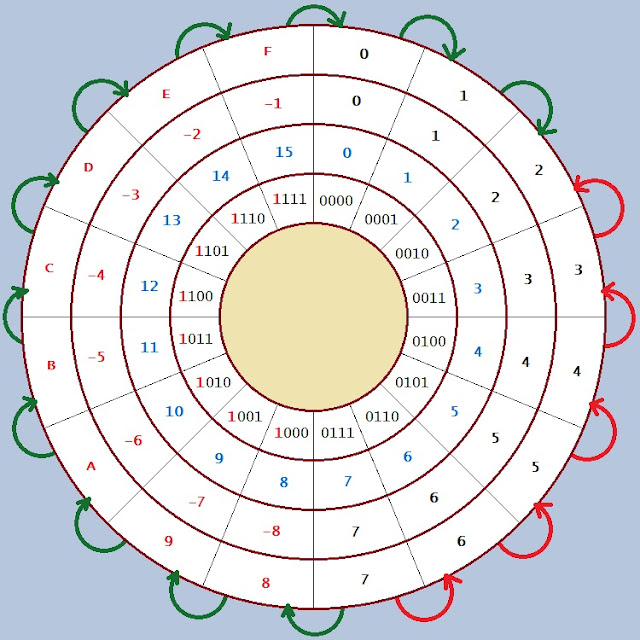
|
| Fig. F - 7 minus 5. |

|
| Fig. G - 7 minus 5 in DEBUG. |
This is the best way I can explain the two's complement to you. Did you like it?

Comments
Post a Comment